(Cette dernière section est un peu plus technique)
Pourquoi faut-il prendre au sérieux cette idée de trou de vers? Parce que la relativité générale d’Einstein, une des théories les plus précises et efficaces jamais conçues, semble presque impliquer leur existence.
La formule ci-dessous (dite métrique de Schwarzschild) est une des solutions fondamentales des équations d’Einstein. Elle décrit la déformation de l’espace-temps autour d’un astre sphérique quelconque de masse M :
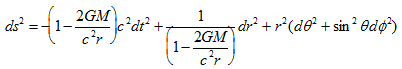
C’est celle qui permet de presque tout faire en relativité générale :
- calculer le mouvement des planètes (en corrigeant les imperfections de la théorie de Newton)
- calculer la forme des mirages gravitationnels
- calculer le retard temporel des signaux voyageant proche des astres
- calculer le décalage vers le rouge des galaxies lointaines
- calculer le rayon et les propriétés des trous noirs
- calculer comment faire fonctionner le GPS en tenant compte des deux effets de ralentissement du temps.
- etc
(Une formule similaire permet de calculer l’évolution de l’univers et ses destins possibles.)
Cette formule de Schwarzschild n’a jamais été prise en défaut, et a été vérifiée de multiples façons, quelquefois à une précision phénoménale. Eh bien, cette même formule, si on examine ce qu’elle dit si le rayon r atteint la valeur 2GM/c2, peut alors impliquer que l’espace courbe se rouvre dans un univers parallèle. Voir le chapitre 8 des notes du cours “Physique Avancée” de Stéphane Durand. (Disponible ici éventuellement).
Peut-on extrapoler de cette façon? On ne le sait pas encore de façon certaine. Mais dans d’autres contextes de l’histoire de la physique, cela a souvent été fait, et quelques fois avec un immense succès:
- Les équations de Maxwell et la prédiction des ondes-radio
- L’équation de Dirac et la prédiction de l’antimatière
- L’équation d’Einstein et la prédiction de l’expansion de l’univers
- Les mathématiques quantiques et la prédictions de la téléportation au niveau atomique
- La théorie mathématique des groupes et la prédictions des quarks (particules constituants le proton et le neutron)
- etc
Remarquez que si la masse est nulle (M = 0) ou si on se trouve très loin de la masse (r → ∞), on retrouve bien la métrique de la relativité restreinte.
Cette métrique de Schwarzschild, très bien établie, conduit toutefois à des trous de vers non-traversables en pratique, entre autres parce qu’ils comportent à leur entrée un trou noir, qui pulvérise par effet de marée tout objet traversant son horizon, et aussi parce qu’ils sont ultra instables.
D’autres métriques semblent possibles, conduisant à des trous de vers traversables (c’est-à-dire stables, sans trou noir et sans horizon), mais elles demandent des effets quantiques pour être réalisées. Les effets quantiques étant bien établis au niveau microscopique, c’est pourquoi il semble très plausible que de tels trous de vers microscopiques existent. Mais peuvent-ils aussi exister au niveau macroscopique? Voilà toute la question…
Voir les notes de cours de Stéphane Durand.